Solutions: Size, Temperature, and Luminosity

Understanding hot plates

1. For each pair of hotplates shown below, circle the one that will boil water more quickly. If there is no way to tell, state that explicitly.
   1. For two hotplates that are the same size, the hotter one will boil the water faster.
   2. For two hotplates that are the same temperature, the larger one will boil the water faster (since the pot is the size of the largest hotplate).
   3. The left-hand hotplate is both hotter and bigger, so it will boil the water faster.
   4. The left hotplate is hotter, but the right hotplate is larger. There is no way to tell which will boil the water faster, without knowing exactly how much hotter the hot hotplate is.

2. If you use two hotplates of different sizes, can you assume that the one that boils water first is at the higher temperature? Which lettered example above supports your answer?

   This is just like (b) above. The hotplates are at the same temperature but the larger one boils water first. It is also like (d) above. For two hotplates of different sizes, you can't necessarily assume that the one that boils water first is hotter. A hot, but very tiny, hotplate might boil water much more slowly than a large, but cooler hotplate.

3. Two students are discussing their answers to Question 2.
   • Student 1: In 1d, the hotplate on the left boils water quicker than the one on the right even though it is smaller. The hotplate's higher temperature is what makes it boil water more quickly.
   • Student 2: But the size of the hotplate also plays a part in making it feel hot. If the hotplate on the left were the size of a pinhead, the water would take a long time to boil. I bet that if the size difference were great enough, the one at the lower temperature could boil the water first.
   Do you agree with Student 1, Student 2, both, or neither? Why?

   I agree with Student 2, because if the "cool" hotplate is only slightly cooler than the "hot" one, but is much larger in size, then the very large (and slightly cooler) hotplate will boil water more quickly than the much smaller (albeit slightly hotter) hotplate.

   The time for the water to come to a boil is determined by the rate at which the element transfers energy to the pot. This rate is related both to the size and temperature of the hotplate. For stars, the rate at which energy is emitted is called luminosity. Similar to the above example, a star's luminosity can be increased by:
   • increasing its temperature; or
   • increasing its surface area (or size).
   This relationship between size, surface temperature, and luminosity allows us to compare the sizes of stars.

4. If two hotplates are at the same temperature and one boils water more quickly, what can you conclude about the sizes of the hotplates?

   If two hotplates are at the same temperature, but one boils water more quickly, then that one is bigger. Both hotplates are transferring the same amount of energy PER UNIT AREA to the pot (which is the size of the largest hotplate, remember!). Therefore the one that boils the water fastest has transferred the most energy to the pot, and must therefore have a LARGER AREA, and be bigger.

5. If two stars have the same surface temperature, and one is more luminous, what can you conclude about the sizes of the stars?

   Similarly, if two stars have the same surface temperature, they are emitting the same amount of energy PER UNIT AREA. If one star is more luminous, that means that it is emitting more total energy. That star must therefore have a BIGGER AREA, and be a bigger star.

   Application to the H-R Diagram

   An H-R diagram represents stars on a graph with luminosity on the vertical axis and surface temperature on the horizontal axis. An H-R diagram is shown below.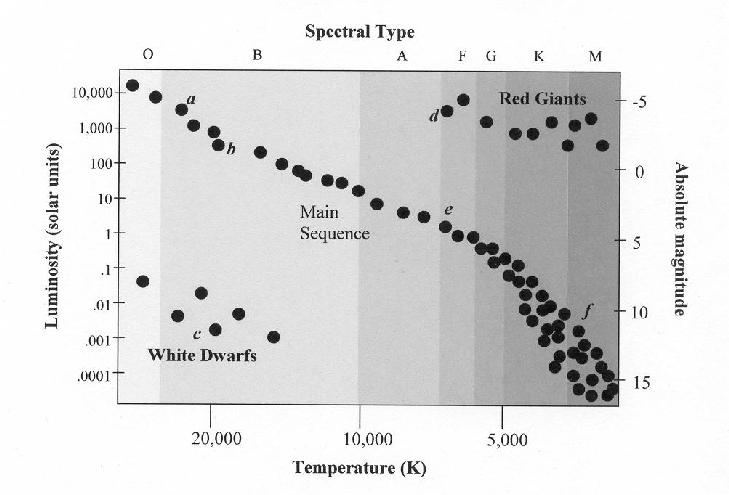 Use the H-R diagram above to answer the following questions.

6. Which star has the same luminosity as the main-sequence star marked a?

   Star d.

7. Which star has the same surface temperature as the main-sequence star marked b?

   Star c.

   Now let's apply what we learned about hotplates to these stars.

8. The pair of stars in Question 6 have the same luminosity, but one is much hotter. What can you conclude about the relative sizes of these two stars?

   Since both stars have the same luminosity, they are emitting the same amount of total energy. Since the cooler star (d) is emitting LESS energy PER UNIT AREA than the hotter star (a), the cooler star must be bigger than the hotter one in order to emit the same amount of total energy.

9. If two stars are the same size, but one is at a higher surface temperature, which star, if either, is more luminous? Explain your answer.

   The hotter star emits more energy PER UNIT AREA than the cooler star. If both stars are the same size, then the hotter star emits more energy in total as well, and is therefore more luminous.

10. The pair of stars in Question 7 have the same surface temperature, but one is much more luminous (ie it is giving off much more energy each second). What can you conclude about the relative sizes of these two stars?

    The more luminous star (b) is bigger than the less luminous star (c). Both stars have the same temperature, and so are emitting the same amount of energy per unit area. But star b is more luminous, and so emitting more energy in total. Therefore, it must have a larger surface area, and be bigger in size.

    Finally, let's remind ourselves of how we get the information required to accurately place a star on the H-R diagram.

11. What measurement of a star must be made in order to determine its surface temperature?

    Measuring the colour (or, more accurately, the wavelength at which a spectrum peaks) gives an indication of the temperature. The relative strengths of the various absorption lines in the spectrum also allow us to refine our estimate of the temperature.

12. To determine the visual luminosity of a star, we need to measure both its distance and one other quantity. What is the other quantity? What method do we use to determine the distance (without using the H-R diagram)?

    We need to measure the distance, and the apparent brightness of the star, in order to determine its luminosity. In order to measure, the distance, we measure its parallax angle (the angle through which the star appears to move against the background stars during a 6-month period).

13. Explain how we can use the H-R diagram to estimate distance if this method is unavailable to us.

    If we cannot use parallax, we analyze the spectrum to measure the temperature of the star, and to determine whether it is a main-sequence star, or red giant, etc. We can then use the star's temperature (and class) to estimate its luminosity from the HR diagram. We can then combine the luminosity with its measured apparent brightness to estimate the distance.