Galaxies: Origin and Evolution(25 points)
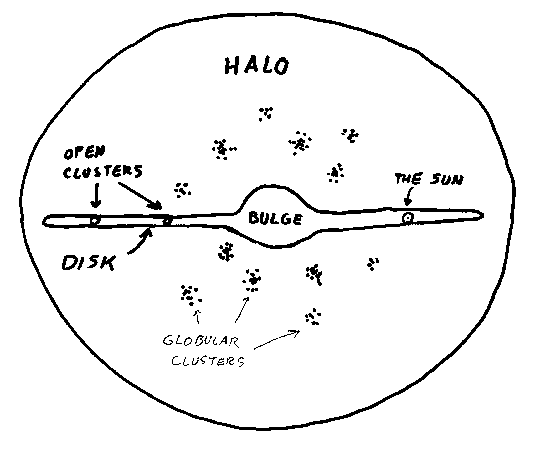
- Draw an edge-on view diagram of our Galaxy. Label all
of the following: disk, halo, bulge, globular clusters, open clusters, and
the location of the Sun.
- How do the orbits, ages, and heavy-element abundances of
the different populations of stars support our basic understanding of
how the Galaxy formed? (i.e. How does the observational evidence match the
predictions of this theory?)
We believe that the halo stars and globular clusters formed early in the collapse of a GIANT swirling cloud of gas and dust, and maintained their orbits as the cloud continued its collapse. The old ages and random orbits of the halo stars support this idea. As the galaxy continued to form, the gas and dust formed a rotating disk (due to conservation of angular momentum), and stars formed at this point will be in the disk. Overall, the disk stars are younger and have circular orbits, which supports this model. We believe that heavy elements are formed only in stars, so the initial cloud of gas and dust must have had very low heavy-element abundances, and as stars synthesize these elements and they are mixed back into the interstellar medium, successive generations of stars will have increasing amounts of heavy elements. The halo stars in general have much lower abundances of heavy elements than the disk stars, which supports our theory since the halo stars formed earliest.
- What observations don't fit into this basic understanding?
Some of the oldest stars are in the bulge, not the halo (which formed first in our model). Some of the youngest globular clusters seem to be farther from the center (in the region that formed first in this model). We don't see as many disk white dwarfs as the theory predicts. Where are the earliest stars that have no heavy elements?
- Why do we believe that galaxy collisions are likely, but
star collisions are not?
We believe that galaxy collisions are likely because typical galaxy separations are only about 20 times the typical size of a galaxy. Stars, however, are typically separated by 10 million stellar diameters!
- What evidence do we have that galaxies collide and merge? Be specific.
The clearest evidence that galaxies collide is found in optical images of interacting galaxies such as The Mice (Figure 13-9), the Whirlpool Galaxy (Figure 13-10) and The Antennae (Figure 13-12). These images show galaxies colliding and the effects of the gravitational forces of each galaxy on the material in them are clearly visible. Additional evidence of collisions is found in the bursts of star formation found in galaxies that have very little gas or dust. Evidence for galactic collisions can also be seen closer to home. The Milky Way is involved in a collision with both the Large and Small Magellanic Clouds (which show evidence of disturbances caused by their interaction with the Milky Way), and the Sagittarius Dwarf galaxy (which is apparently being destroyed by and absorbed into the Milky Way. Collisions between galaxies is also indicated by ring galaxies which appear to originate when two galaxies collide head on at high speed. Many ring galaxies do have nearby companions.
Galaxies: Mass and Dark Matter (20 points)
(Mathematically, the expression for the mass enclosed within an orbit
of radius r is M = v2r/G, where G is Newton's
gravitational constant (numerically equal to
4.30 x 10-6(kpc/M )·(km/s)2) and v is the orbital speed of a star at
distance r. This formula is essentially another way of writing Kepler's
Law Porb2 = constant * r3.)
)·(km/s)2) and v is the orbital speed of a star at
distance r. This formula is essentially another way of writing Kepler's
Law Porb2 = constant * r3.)
This concept works equally well for the orbits of stars and gas within spiral galaxies. By looking at the mass inside the orbit of stars or gas at different distances from the center of the galaxy, the mass of a galaxy as a funcion of radial distance from the center (the mass of a galaxy INSIDE radius r) can be obtained from the rotation curve of the galaxy.
Basically, both when discussing the orbits of planets around a star, or the orbits of stars around the center of the galaxy, the mass inside the orbit determines, via gravity, the properties of the orbit. The difference here is that if you look at a bigger orbit (farther from the center), the mass inside that orbit is bigger than the mass inside the smaller orbit (something that doesn't happen with different-sized orbits around stars - remember that the mass of the planets is insignificant compared to the mass of the star).
Measuring the Mass
- Compared with rotation curve B, does rotation curve A yield a larger,
or smaller, mass for the Milky Way Galaxy within a radius of 8 kpc? Why
(include words)?
(Hint: This is equivalent to asking, "What would happen to the
speed of the Sun's orbit around the Galactic Center if the mass enclosed
were larger or smaller than it is?")
Rotation curve A yields a smaller mass for the Milky Way Galaxy within a radius of 8 kpc. If a higher mass is enclosed within the same radius, the gravitational force on the orbiting (much less massive) object is larger, and the orbital velocity required to keep it in orbit (rather than falling) is larger. Rotation curve B has a larger velocity at 8kpc, and so a larger mass inside 8 kpc is inferred.
( Bonus: By what factor? (You can use ratios to solve this, or calculate the mass within 8 kpc in each case.))
Since mass is proportional to velocity squared (v2), and the velocity of curve A at 8 kpc is about half that of curve B at 8 kpc, the mass inferred from curve A is one quarter that inferred from curve B.
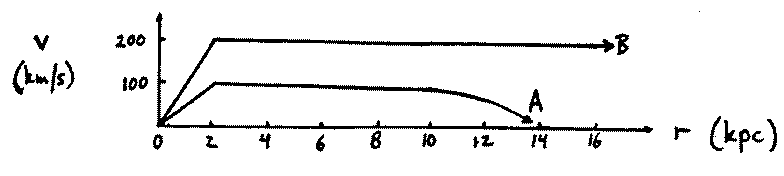
Shown above are two possible rotation curves of the Milky Way Galaxy. (Neither one is necessarily correct.)
Dark Matter!
- Once you look at stars which are far enough out that essentially all
of the mass is inside their orbit, what happens to the orbital velocity
of stars/gas as you keep looking at stars farther from the center? (Note that
the mass enclosed within radius r is no longer changing.) Which curve would
be true in this case? (Hint: Think about the orbital velocities of
planets at different distances from the Sun).
Once the radius is large enough to enclose all of the mass of the galaxy, the mass will no longer increase as the radius (from the galaxy's center) increases. In this case, as you move further out, the force of gravity decreases (the mass stays the same, but the distance to the center increases), and so the velocity required to stay in orbit about the galaxy (rather than fall in) decreases. In this case, rotation curve A would have to be true.
- We know that the luminous
material (stars, gas) in the Milky Way Galaxy extends out to a radius of
14 kpc, and becomes quite faint beyond that. Suppose rotation curve B is
correct. Does this match your prediction in part (b)? If not, what must
be true at radii larger than 14 kpc? Why?
(Hint: If the mass was traced by the luminous matter, how much would
the mass enclosed increase as you go beyond 14 kpc? What what would happen
to the velocity outside 14 kpc? Your answer to the part (b) of this
question will help here).
If the luminous material does not extend beyond 14kpc, and this material accurately traced the mass, then the mass would not increase as the radius increased. In this case, according to part (c), the velocity would decrease beyond 14 kpc, and rotation curve A would be true. But this question assumes that rotation curve B is correct! Therefore there must be mass beyond 14 kpc that we cannot see: Dark Matter!
The rotation curve of the Milky Way Galaxy is more like curve B than curve A! So there is matter that we cannot see: Dark Matter! In fact, only about 1% to 10% of our Galaxy's mass is luminous.
We have also applied this method to other spiral galaxies. We can estimate the the expected mass of a galaxy based on its brightness and distance. This gives us an estimate of the mass of the luminous matter in the galaxy. The rotation curve method tells us the mass based on the gravitational influence of all the mass in the galaxy. For most galaxies, the luminous mass is in the neighbourhood of 10 times less than the mass determined from the rotation curve method. Therefore, a significant fraction of the mass of the galaxy must be in dark matter.
Additional evidence comes from X-ray observations of hot gas in galaxy clusters, which would escape if the clusters only contained the mass inferred from the luminous matter in its galaxies (since high temperatures mean fast-moving particles). Similarly, the high velocities within the clusters of the galaxies themselves indicates the presence of substantial dark matter. Finally, gravitational lensing indicates the presence of dark matter in galaxy clusters.
All methods of measuring the masses of galaxies use some measurements of velocity and size (which requires distance!), combined with the laws of gravity. For example, measuring galaxy masses using rotation curves for spiral galaxies involves knowing the rotational velocity of stars/gas in the galaxy's disk (from Doppler shifts) at various distances from the center (so we need to know the distance to the galaxy), along with the assumption that the orbits of these stars/gas clouds are determined by the mass lying inside their orbits.
Another method involves looking at the widths of absorption lines in the galaxy overall. These widths allow us to estimate the overall motions of the gas in the galaxy, and we can therefore infer the mass that would be required to keep this gas inside the galaxy? This method gives less detailed information, but still involves a measurement of velocity, an estimate of the galaxy's size, and the assumption that gravity is the only thing keeping this moving material inside the galaxy.
Equivalently, the motions of galaxies or gas in a cluster of galaxies can be used to estimate the mass of the total cluster. Dividing the mass of the cluster by the number of galaxies gives the average mass of each galaxy. Once again, there is not detailed information, but we have measured masses.
Note that measuring the mass in these ways is different from adding up the mass expected from the luminous matter in the galaxy. That is merely an educated guess, based on our knowledge of the masses of objects we can see.
Galaxies: Distances (30 points)
- For one of these, explain how we can use these objects to determine the
distances to galaxies. (What property of a standard candle (or ruler) allows
us to determine the distance, and how? What measurements must be made in
order to determine the distance?)
"Standard candles" are objects of known luminosity. Once we know the luminosity of a particular kind of object, we can combine that knowledge with the observed apparent brightness of the object to infer its distance. Cepheid variable stars are an example of this kind of object: by measuring the period of such a variable star, we can determine its average luminosity by using the "Period-Luminosity" relation for this kind of star. Combining this with its average apparent brightness allows us to determine the distance by using the inverse square law of light (more distant objects appear dimmer).
"Standard rulers" are objects of known size. If we know the size of an object, we can combine that knowledge with its observed apparent size in order to infer its distance. More distant objects appear smaller. There are no really good "standard rulers", but in general, the galaxies in a more distant cluster will appear smaller than those in a nearby cluster.
- Explain why calibrating these standard objects is required,
and what is involved. (Hint: We discussed this issue when we talked
about using spectroscopic parallax to determine the distances to stars.)
We must calibrate these standard objects in order to determine their intrinsic luminosity (in the case of standard candles) or absolute size (in the case of standard rulers). For example, in order to use the Period-Luminosity relationship for Cepheid variables (see above), we must first determine this relationship. In order to do this, we must KNOW the luminosity of several Cepheid variables, and to do this we must first know their distance. All distance-finding methods involving standard candles must be calibrated using a previous method.
Hubble's Law says that the expansion of space between the galaxies is simply v = Hod, where v is the apparent recessional velocity of a galaxy, Ho is the Hubble constant, and d is the distance of the galaxy.
- What observations are necessary in order to determine the Hubble
constant? (Hint: What properties of galaxies do we need to measure?
For just one galaxy, or for many?)
In order to determine the Hubble constant, we need to measure both the distances and recessional velocities of many galaxies.
- What sorts of observations do we need to make to determine these
quantities? Which is the most difficult to measure?
The recessional velocities can be determined by measuring the Doppler shift of absorption lines. This is straightforward and reasonably accurate. Distances, however, are extremely difficult to determine because the most direct method, parallax, is only useful for nearby stars within our own galaxy. All other methods must be calibrated before they can be used. This is a time consuming and difficult process, and as a result there are large uncertainties in the measured distances. In addition, gas and dust can dim the light from distant objects. This can further distort distances measured using standard candles. The Hubble Space Telescope was built to improve our measurements of distances to galaxies, and has improved our determination of the Hubble constant.
- Assume that you have now measured the Hubble constant. (In
essence, you have now calibrated Hubble's Law). How do
the large redshifts of quasars lead us to conclude they must be very
distant?
Quasars show large red shifts in their spectra. One way to interpret this is with the use of the Hubble law which relates the recessional velocity of distant galaxies to their distance. The red shifts are attributed to the Doppler effect, and provide a measurement of the recessional velocities of the quasars. The technique only works for distant galaxies, objects outside of the Local Group. However, it provides a direct method for determining the distance to an object whose red shift is known (and is due to the expansion of the universe). The large redshifts observed in quasars (in excess of z=0.1) imply that the quasars are at distances in excess of 400 Mpc (assuming that H = 70 km/s/Mpc).
- If a star in our own Milky Way Galaxy is measured to have a
redshifted spectrum, can the redshift be used with Hubble's law to determine
the distance to that star?
No, Hubble's law is only valid on the large scales where the space between the galaxies is expanding. Locally, like within the Galaxy, gravity is holding everything together and the expansion of space is not observable. So redshifts measured for stars within the Galaxy only tell you about the speed at which that star is moving away, and nothing else.
Galaxies: Centers (25 points)
First, the evidence that quasars are really as distant as their redshifts imply. Absorption lines in some quasar spectra are at the same redshift as a foreground galaxy, indicating that the quasar is more distant. Gravitational lensing of quasars (producing multiple images of a single quasar) implies the quasar is at a greater distance than the galaxy or material causing the lensing.
Now the evidence that quasars occur in distant galaxies: In images of some quasars, a faint "fuzz" is seen around the quasar, which is believed to be the galaxy surrounding the quasar (which is an extremely active nucleus). The spectra of such "fuzz" are similar to spectra of other distant galaxies. Secondly, a supernova was detected near QSO 1059+730. The rest of the galaxy was too faint to be detected, but this does indicate that the quasar and supernova were in the same galaxy. Finally, quasar 3C 273 shows jets of material very similar to those seen in some other galaxies.
The core of the galaxy appears to be a very energetic source of energy for several reasons. First, the gas that is very close to the core is highly ionized, indicating that extremely high temperatures exist in this region. This suggests that the core produces large amounts of x-ray, ultraviolet, and possibly gamma-ray radiation. Secondly, radio observations have shown the presence of a small, luminous radio source at the center, as well as matter apparently swirling around this source. Radio observations have also shown large powerful jets emanating from the core. Such jets require high energy phenomena to produce them. Finally, the rapid motions of the hot gas, cool clouds, and stars in the vicinity of the core suggest that it is extremely massive and very compact.
- Briefly describe the unified model that explains Active
Galactic Nuclei and quasars. (i.e. What is causing the extraordinary
activity?)
The "unified model" consists of a supermassive black hole at the centers of these galaxies. The black hole is surrounded by an accretion disk of infalling matter, which is accompanied by jets of matter and radiation perpendicular to this disk.
- In this model, what role do collisions and mergers play in triggering
active galaxies?
In the unified model, the unusually strong activity at the galaxy's center is triggered by a galaxy interaction, collision, or merger, as these disrupt the galaxies and push extra material toward the supermassive black hole. The increased material falling into the black hole results in increased emission of radiation.
- What evidence do we have that quasars must be triggered by collisions
and mergers?
Many quasars are found in tidally distorted galaxies which suggests mergers, collisions, and interactions of the parent galaxies. Such interactions could throw large amounts of material toward the black hole and form the accrtion disk that seems necessary to produce a quasar.
- Bonus: Why are there few quasars at low red shifts and at high red
shifts, but many at red shifts of about 2?
At low red shifts (nearby: z < 1), the distribution of galaxies is fairly scattered and interactions between the galaxies is not extremely common. At high red shifts (most distant: z > 4: early in universe's history), few galaxies had formed, so few interactions between them could take place. However, at distances associated with red shifts of about z = 2, galaxies were prevalent and they were fairly close together, so that they collided more often than they do at the present time (low red shifts).