Seasons (25 points)
- Do the Pongians in the northern hemisphere experience seasons? Why or
why not?
Although Pong's rotational axis and orbital axis are aligned (ie it doesn't have a tilt like the Earth does), Pong's orbit around its sun is very elliptical. For this reason, Pong is significantly closer to its sun at one part of its orbit, and significantly farther at another. When Pong is closer to its sun, it receives more energy from its sun, and the weather is warmer -- summer. When Pong is farther from its sun, it receives less energy, and the weather is cooler -- winter.
- Is the seasonal (or otherwise) experience of those in the northern and
southern hemispheres of Pong the same (at the same time)? Why or why not?
All of Pong is closer to its sun during the Pongian summer, so the seasonal experiences of those on all parts of Pong is the same.
- Does the compass position of the rising (or setting) of their blue sun
vary throughout the Pongian year? Explain why or why not.
The compass position of the rising/setting of the blue sun does NOT vary throughout the Pongian year. This is because Pong has no axial tilt, so the position of Pong's sun doesn't vary relative to Pong's equator throughout the year. Pong's sun always lies on the celestial equator (unlike our sun), and so it always rises exactly in the east, and sets exactly in the west.
- Does the Pongian period of daylight change during the year? Why or why
not?
Because Pong has no axial tilt, the days are the same length at all times throughout the year - equal to half the time taken for one revolution (spin) of Pong relative to its Sun. The changing hours of daylight on earth are caused by the changing orientation of the tilted earth relative to the sun.
- Is the Pongian climate the same at its poles as its equator? Why or why
not?
As we saw in part (b), because there is no axial tilt, the length of the Pongian day is the same in both winter and summer, and the same all over Pong. As we saw in Question 1 (b), all of Pong experiences winter and summer reaches the ground is not the same all over Pong. The blue sunlight shines directly down on the ground at the equator, but at a very large angle at the poles (in fact, at the Pongian poles, the blue sun is always on the horizon!). Thus the poles are always cooler than the equator.
Phases of the Moon (20 points)
To do this question, it might help you to first:
- Locate an Earth-bound observer at sunset on the following diagram.
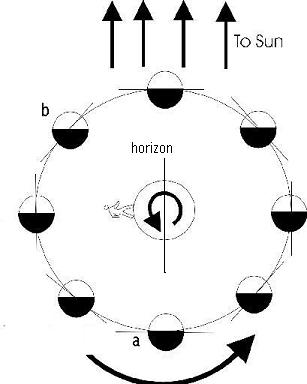
Briefly explain your answers for parts (a) and (b)
The image above is all you need to figure out the problem. It shows the Earth, Sun, and Moon for several times during the month. I have placed the observer at sunset in the diagram. The sun is just rotating out of view from his perspective, which means it is sunset (notice the small arrow indicating the direction of the Earth's rotation). In the diagram above, the portion of the moon that is visible is the half which is inside the tangent to the circle representing its orbit (ie the half that is facing the observer). As the month progresses, the moon moves from position to position according to the direction of the large arrow.
(a) If the moon is near the eastern horizon, then it is nearly opposite the sun (which is in the west), and so it must be at the position labelled (a). We can see pretty much all of the lit side of the moon, and so it is basically full. (I'm assuming it's just after the sun has set).
Aside: If the moon were higher above the eastern horizon, it would be in its "gibbous" (more than half-lit) phase. The moon is becoming increasingly full during this part of the month (large arrow), and so it is "waxing". So the phase of the moon is "waxing gibbous", and it would be mostly lit, with only a small portion on its eastern side unlit.
(b) If the moon is in the southwest, it must be at position (b) in the diagram (ie near the sun, but above the observer's horizon). We can only see a small portion of the lit side of the moon, so it is not yet half full (which would be first quarter - one quarter of the way around the orbit). So it is in the "crescent" phase. Once again it is increasing in fullness each night (waxing), so the moon is waxing crescent, and only a portion of its western side would be lit. Note that the higher the moon is above the horizon, the fatter the crescent will be.
During a new moon the moon is in the direction toward the sun. As it progresses, it moves toward the east. So just after the new moon, the moon will be a little bit to the east of the sun in the sky, but still very close to it. The only time the moon would be visible this close to the sun is if the sun was below the horizon, but the moon was not. If the moon is a little bit to the east of the sun, you'd need to look in the west just after sunset.
When the moon is near the new moon, an observer on the moon would see the fully illuminated "full earth". The light from the "full earth" can illumnate the otherwise dark regions of the moon, resulting in a faint glow on the dark portion of the moon. This glow is called earthshine.
Eclipses (15 points)
- What phase will the moon be in during each eclipse?
During a total solar eclipse, the Sun's light is blocked from the view of some observers by the Moon's shadow. Therefore total solar eclipses only happen at new moon. In a total lunar eclipse, the earth's shadow blocks the light from the Sun so that it does not reach the moon. Therefore total lunar eclipses only happen at full moon.
- Will the total solar eclipse be visible to all observers on the day side
of the earth at the time of the solar eclipse? Why or why not?
A total solar eclipse is only visible to those observers on the portion of Earth which is completely shadowed by the Moon. The moon's shadow (umbra) is not large enough to cover the entire earth. Other observers may see a partial eclipse because the moon partially shadows their location. Light from certain portions (but not all) of the Sun is blocked, so these observers are in the penumbra.
- Will the lunar eclipse be visible to all observers on the night side of
the earth at the time of the lunar eclipse? Why or why not?
The lunar eclipse will be visible to all observers who are in night at that time. The Earth is shadowing the entire moon, and so anyone seeing the moon at that time will see it in shadow.
- Extra Credit: Will the moon be visible during the lunar eclipse?
Why or why not?
The moon will be visible during the eclipse, although it will be much dimmer and redder. This is because the Earth's atmosphere redirects some sunlight (mostly red) into the shadow. This redirected light illuminates the moon during the eclipse.
Choosing Between Models (20 points)
As we saw in class, the retrograde motion of the planets (such as Mars) can be equally well explained by two competing models for the Solar System: the Ptolemaic (Earth stationary at the center) model, and the Copernican (Sun-centered) model. Here we explore an observation that forces us to choose the Sun-centered model over the Earth-centered one!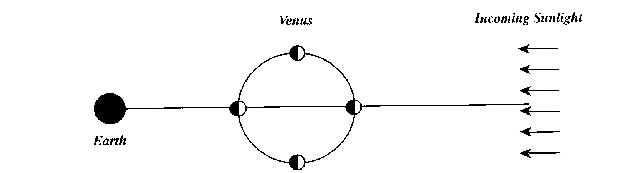
- (5 points) Shade the portion of Venus not illuminated by
the Sun (here or on a copy). Remember that the Sun is very far away!
Can a "full" Venus ever be seen from the Earth in this model? Why?
A full Venus can never be seen in this model. This is because Venus is always between the Earth and the Sun, and the side of Venus facing the Sun is the lit side. As the diagram above shows, only a small portion of the illuminated side of Venus is ever visible from the Earth in this model.
Galileo Galilei was the first person to use a telescope to observe Venus. Over time, he noted that Venus exhibited phases, as shown below:
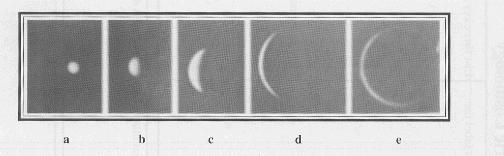
Galileo knew of the Sun-centered, or heliocentric model developed by Nicolaus Copernicus. Galileo found that this model was able to completely explain the observed phases of Venus.
- Using the diagram below (or a copy), place Venus in the positions needed
to produce the phases seen in panels a and e. Label these positions with a
and e.
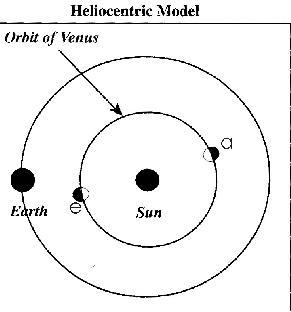
- Briefly explain how the heliocentric model accounts for the observed
phases of Venus.
In the heliocentric model, the illuminated side of Venus is always facing the Sun. Sometimes this side is visible from the Earth (as in position a), and Venus appears full. At other times, only a portion of the illuminated side of Venus is visible from the Earth (e), and Venus appears to be only partially illuminated. We see a complete range of Venus' phases in this model because Venus and the Earth are not always on the same side of the Sun.
- Briefly explain how the sizes of the images of Venus in panels a
and e are explained by this model.
In this model, Venus appears most full when it is furthest away (on the opposite side of the Sun from the Earth). Venus appears least full when it is closest to the Earth (on the same side of the Sun). Since more distant objects appear smaller than closer objects of the same size, the full Venus (panel a) appears smallest, and the crescent Venus (panel e) appears largest.
Orbits and Gravity (20 points)
- You are on the planet Pong, which is the same size as the Earth, but has 2 times the mass.
- You are on the planet Quing, which has the same mass as the Earth, but is only half as large.
- Extra Credit: What is your mass in parts a-b (compared to your current mass)?
I worded the question poorly. I should have stated more explicitly that an object's weight on a planet's surface is the force that this planet's gravity exerts on the object. Therefore your weight on the Earth's surface is GMm/R2, where M and R are the mass and radius of the earth, and m is your mass. Since Pong is identical to the Earth, except that it has 2 times the mass of the Earth, the force (on you) due to the gravity of Pong is greater, so your weight would be greater.
Specifically, the force of Pong's gravity on you is G(2M)m/R2, which is 2 times larger than on Earth (comparison!). Therefore you would weigh twice as much as you do now.
Since Quing has the same mass as the Earth, but is only half as large, the force of gravity exerted by Quing on you is greater than on Earth. Remember that the force of gravity decreases with distance, so if we decrease the distance to the center of the planet, the force must increase. Therefore your weight increases.
To be specific, Quing's force of gravity on you is GMm/(R/2)2, which is GMm/(R2)/4 = 4GMm/R2. This is 4 times as much force as Earth exerts on you (compare them!), and so you would weigh 4 times as much on Quing as you do on Earth.
You mass in all three parts remains unchanged. The amount of material in your body hasn't changed, just the force of gravity that the planets exert on you.
- Is a Quingan year longer or shorter than an Earth year (ie Does Quing have a longer or a shorter orbital period than the Earth)? Explain in terms of gravity. (Hint: Does Quing need to go faster or slower than the Earth in order to maintain its orbit? Why?)
- The Quingan people have discovered another planet (called Zampa) which orbits their star at a distance of 4 AU. Is a Zampan year longer or shorter than a Quingan year? Explain in terms of gravity.
Because a planet is always MUCH less massive than the star around which is circles, the mass of the planet can be neglected from consideration. Since Quing lies 1 AU away from its blue star, it is at the same distance from its star as the Earth is from the Sun. But its blue sun is twice as massive as our sun. Therefore, Quing experiences a stronger gravitational pull from its star than the Earth does from our Sun (twice as strong, in fact). Quing must therefore move faster in order to stay in orbit. So the Quingan year is shorter than the Earth year.
(For those who care, the period P and size a of a
planet's orbit, and the mass of a star are related by
P2 =
4 2/Gmstar * a3.
2/Gmstar * a3.
Since the Quingan and Earth orbits are the same size, while the
Quingan star's mass is twice that of our sun, you can write down the
equation for both the Earth and Quing, compare them, and learn that the
Quingan year is 1 Earth yr/sqrt(2)i, or about 0.7 Earth years.)
Zampa orbits the Quingan star at a distance of 4 AU, which is 4 times further from their sun than Quing itself. Therefore their star exerts less gravity on Zampa than on Quing. Therefore Zampa doesn't have to move as fast as Quing in order to stay in orbit. Zampa also has further to travel in order to go once around the blue star! So it is going slower, and has farther to go, so it's year must be longer!
(For those who want to know exactly, by writing down the equation
in part (a) for both Quing and Zampa, and comparing them
(only the variable "a" changes!), you find that the Zampan
year is
PZ =
PQ * (aZ / aQ)1.5 =
8 Quingan years!)