Galaxies: Origin and Evolution(25 points)
- Draw an edge-on view diagram of our Galaxy. Label all of the following: disk, halo, bulge, globular clusters, open clusters, and the location of the Sun.
- How do the orbits, ages, and heavy-element abundances of the different populations of stars support our basic understanding of how the Galaxy formed? (i.e. How does the observational evidence match the predictions of this theory?)
- What observations don't fit into this basic understanding?
- Why do we believe that galaxy collisions are likely, but star collisions are not?
- What evidence do we have that galaxies collide and merge? Be specific.
Galaxies: Mass and Dark Matter (20 points)
(Mathematically, the expression for the mass enclosed within an orbit
of radius r is M = v2r/G, where G is Newton's
gravitational constant (numerically equal to
4.30 x 10-6(kpc/M )·(km/s)2) and v is the orbital speed of a star at
distance r. This formula is essentially another way of writing Kepler's
Law Porb2 = constant * r3.)
)·(km/s)2) and v is the orbital speed of a star at
distance r. This formula is essentially another way of writing Kepler's
Law Porb2 = constant * r3.)
This concept works equally well for the orbits of stars and gas within spiral galaxies. By looking at the mass inside the orbit of stars or gas at different distances from the center of the galaxy, the mass of a galaxy as a funcion of radial distance from the center (the mass of a galaxy INSIDE radius r) can be obtained from the rotation curve of the galaxy.
Basically, both when discussing the orbits of planets around a star, or the orbits of stars around the center of the galaxy, the mass inside the orbit determines, via gravity, the properties of the orbit. The difference here is that if you look at a bigger orbit (farther from the center), the mass inside that orbit is bigger than the mass inside the smaller orbit (something that doesn't happen with different-sized orbits around stars - remember that the mass of the planets is insignificant compared to the mass of the star).
Measuring the Mass
- Compared with rotation curve B, does rotation curve A yield a larger,
or smaller, mass for the Milky Way Galaxy within a radius of 8 kpc? Why
(include words)?
(Hint: This is equivalent to asking, "What would happen to the
speed of the Sun's orbit around the Galactic Center if the mass enclosed
were larger or smaller than it is?")
( Bonus: By what factor? (You can use ratios to solve this, or calculate the mass within 8 kpc in each case.))
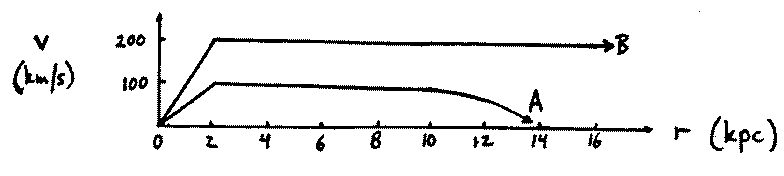
Shown above are two possible rotation curves of the Milky Way Galaxy. (Neither one is necessarily correct.)
Dark Matter!
- Once you look at stars which are far enough out that essentially all
of the mass is inside their orbit, what happens to the orbital velocity
of stars/gas as you keep looking at stars farther from the center? (Note that
the mass enclosed within radius r is no longer changing.) Which curve would
be true in this case? (Hint: Think about the orbital velocities of
planets at different distances from the Sun).
- We know that the luminous
material (stars, gas) in the Milky Way Galaxy extends out to a radius of
14 kpc, and becomes quite faint beyond that. Suppose rotation curve B is
correct. Does this match your prediction in part (b)? If not, what must
be true at radii larger than 14 kpc? Why?
(Hint: If the mass was traced by the luminous matter, how much would
the mass enclosed increase as you go beyond 14 kpc? What what would happen
to the velocity outside 14 kpc? Your answer to the part (b) of this
question will help here).
The rotation curve of the Milky Way Galaxy is more like curve B than curve A! So there is matter that we cannot see: Dark Matter! In fact, only about 1% to 10% of our Galaxy's mass is luminous.
We have also applied this method to other spiral galaxies. We can estimate the the expected mass of a galaxy based on its brightness and distance. This gives us an estimate of the mass of the luminous matter in the galaxy. The rotation curve method tells us the mass based on the gravitational influence of all the mass in the galaxy. For most galaxies, the luminous mass is in the neighbourhood of 10 times less than the mass determined from the rotation curve method. Therefore, a significant fraction of the mass of the galaxy must be in dark matter.
Galaxies: Distances (30 points)
- For one of these, explain how we can use these objects to determine the distances to galaxies. (What property of a standard candle (or ruler) allows us to determine the distance, and how? What measurements must be made in order to determine the distance?)
- Explain why calibrating these standard objects is required, and what is involved. (Hint: We discussed this issue when we talked about using spectroscopic parallax to determine the distances to stars.)
Hubble's Law says that the expansion of space between the galaxies is simply v = Hod, where v is the apparent recessional velocity of a galaxy, Ho is the Hubble constant, and d is the distance of the galaxy.
- What observations are necessary in order to determine the Hubble constant? (Hint: What properties of galaxies do we need to measure? For just one galaxy, or for many?)
- What sorts of observations do we need to make to determine these quantities? Which is the most difficult to measure?
- Assume that you have now measured the Hubble constant. (In essence, you have now calibrated Hubble's Law). How do the large redshifts of quasars lead us to conclude they must be very distant?
- If a star in our own Milky Way Galaxy is measured to have a redshifted spectrum, can the redshift be used with Hubble's law to determine the distance to that star?
Galaxies: Centers (25 points)
- Briefly describe the unified model that explains Active Galactic Nuclei and quasars. (i.e. What is causing the extraordinary activity?)
- In this model, what role do collisions and mergers play in triggering active galaxies?
- What evidence do we have that quasars must be triggered by collisions and mergers?
- Bonus: Why are there few quasars at low red shifts and at high red shifts, but many at red shifts of about 2?